The Art of Interface

Article 11 — Appendix A.1

abs — absolute value function

Category. Mathematics.

Abstract. Absolute value: definition, plot, properties and identities.

Reference. This article is a part of Librow scientific formula calculator project.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows

1. Definition

Absolute value function is defined as

|x| = x for x ≥ 0;
|x| = −x for x < 0.

2. Plot

Absolute value function is defined everywhere on real axis. Its plot is depicted below — fig. 1.

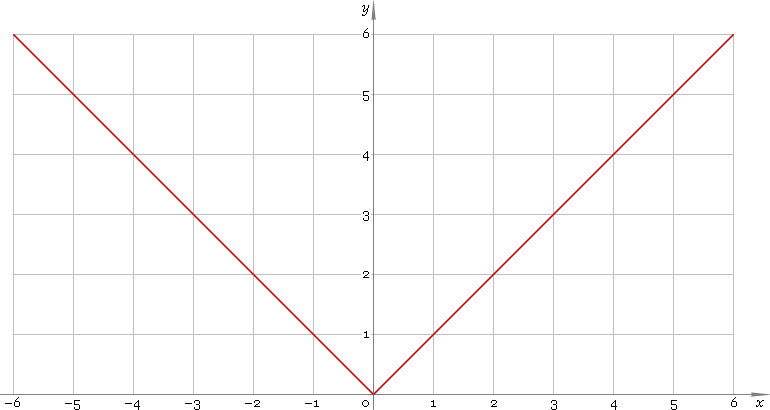Fig. 1. Plot of the absolute value function y = |x|. Fig. 1. Plot of the absolute value function y = |x|.

Function codomain is non-negative half of the real axis: [0, +∞).

3. Identities

Function is symmetrical:

|−x| = |x|

Sum and difference of arguments:

|x + y| = |x| + |y|, if signx = signy
|x + y| = ||x| − |y||, if signx ≠ signy
|x − y| = ||x| − |y||, if signx = signy
|x − y| = |x| + |y|, if signx ≠ signy

Product and ratio of arguments:

|xy| = |x||y|
|x /y| = |x| /|y|

4. Support

Absolute value function abs of the real argument is supported by free version of the Librow calculator.

Absolute value function abs of the complex argument is supported by professional version of the Librow calculator.

5. How to use

To calculate absolute value of the number:

abs(-1);

To calculate absolute value of the current result:

abs(rslt);

To calculate absolute value of the number x in memory:

abs(mem[x]);