The Art of Interface

Article 11 — Appendix A.36

I — modified Bessel function of the first kind

Category. Mathematics.

Abstract. Modified Bessel function of the first kind of the real (fractional) order: definition, plot, properties and identities.

Reference. This article is a part of Librow professional formula calculator project.

See also. Kν — modified Bessel function of the second kind, Jν — Bessel function of the first kind.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows

1. Definition

By definition modified Bessel function is solution of the modified Bessel equation

z2 w′′ + z w′ − (z2 + ν2) w = 0

As second order equation it has two solutions, first of which has no singularity at 0 and is called modified Bessel function of the first kind — Iν. Parameter ν is called order of the function.

Second solution has singularity at 0 and is called modified Bessel function of the second kind — Kν.

2. Plot

Modified Bessel functions of the first kind defined everywhere on the real axis, so, their domain is (−∞, +∞). Plots of the first three representatives of the first kind modified Bessel function family depicted below — fig. 1.

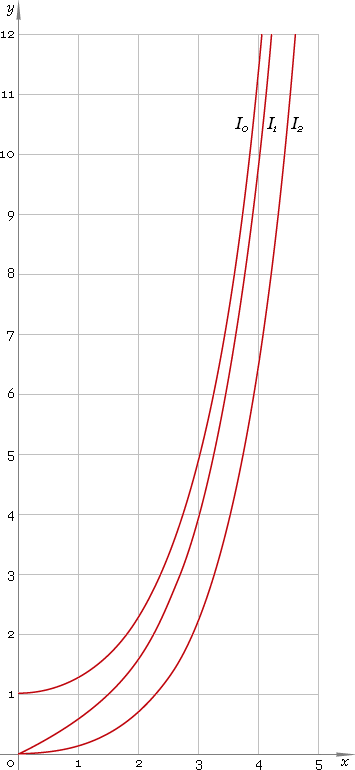Fig. 1. Plots of the modified Bessel functions of the first kind y = I0(x), y = I1(x), y = I2(x). Fig. 1. Plots of the modified Bessel functions of the first kind y = I0(x), y = I1(x) and y = I2(x).

3. Identities

Connection to the ordinary Bessel function of the first kind:

Iν(z) = (−i)νJν(iz)

Connection to the modified Bessel function of the second kind:

I−ν(z) = Iν(z) + 2 /π sin(πν) Kν(z)

Next order recurrence:

Iν+1(z) = −2ν /z Iν(z) + Iν−1(z)

Negative argument:

Iν(−z) = eiπν Iν(z) = [cos(πν) + i sin(πν)] Iν(z)

For the case of integer order ν=n the negative argument identity can be simplified down to:

In(−z) = (−1)n In(z)

and for the case of half-integer order ν=n+1/2 the identity can be simplified down to:

In+1/2(−z) = i (−1)n In+1/2(z)

Reflection — negative order:

I−ν(z) = Iν(z) + 2 /π sin(πν) Kν(z)

For the case of integer order ν=n reflection identity can be simplified down to:

I−n(z) = In(z)

and for case of half-integer order ν=n+1/2 the identity can be simplified down to:

I−n−1/2(z) = In+1/2(z) + (−1)n 2 /π Kn+1/2(z)

4. Support

Modified Bessel function of the first kind Iν of the real (fractional) order and complex argument is supported by professional version of the Librow calculator.

5. Interface

Modified Bessel function call looks like

I(order, argument);

or

BesselI(order, argument);

where order is the function real order, and argument — function argument.

6. How to use

To calculate modified Bessel function of the first kind of the 0 order of the number:

I(0, -1.5+i);

or:

BesselI(0, -1.5+i);

To calculate modified Bessel function of the first kind of the 1.2 order of the current result:

I(1.2, rslt);

or:

BesselI(1.2, rslt);

To calculate modified Bessel function of the first kind of the 2.5 order of the number z in memory:

I(2.5, mem[z]);

or:

BesselI(2.5, mem[z]);